~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
|  Cornell SSW: Mathematica == Fun(ctions).  |
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Monday March 27, 2017

Author: Varun Gandhi (vg266) - Physics first year grad student

Obligatory feature list:
* Functional programming - first-class functions, lambdas, map, select etc.
* Symbolic manipulation - solving differential equations, nasty integrals etc.
* Rich visualization tools - making pretty graphs is relatively painless (glares at TikZ/PGF)
* Batteries + supercharger included - lots and lots of performant in-built functions
* Good documentation - easy to access with many examples
* Rapid prototyping - consequence of abovementioned features
* Getting help - friendly StackExchange community
and many more (depending on your field).

(Benchmarks: http://julialang.org/benchmarks/)

Example 1: You can make a fake alien language for a popular science fiction movie
(which is unfortunately unlike that in the original short story).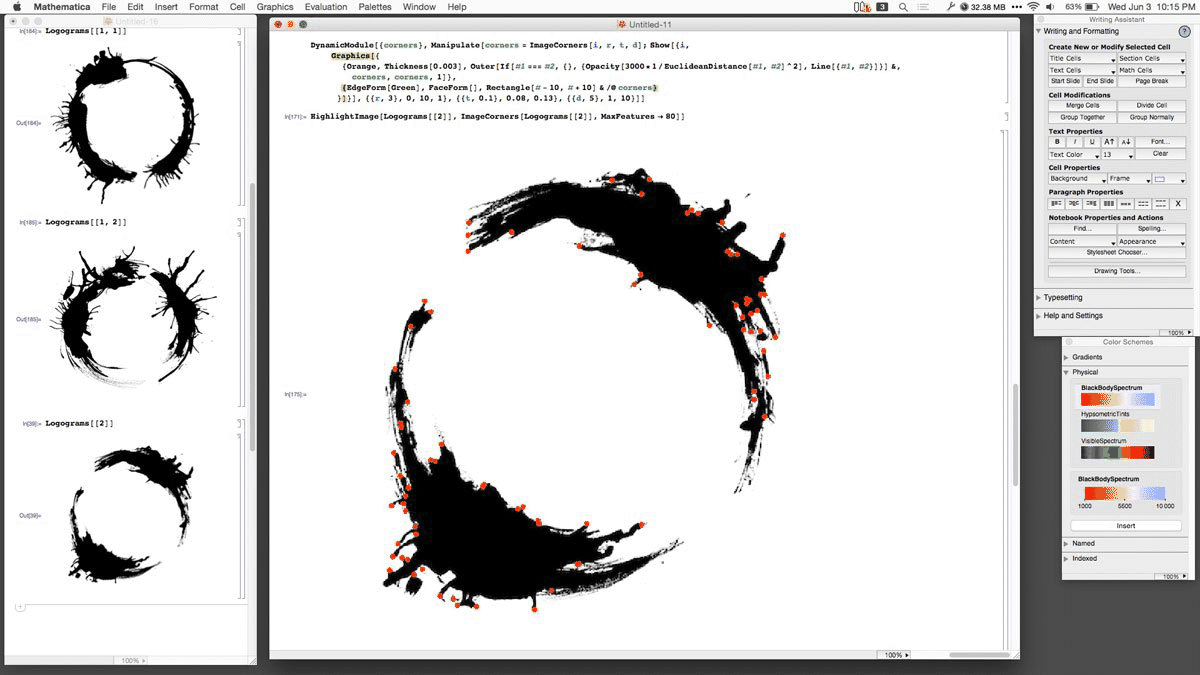

Example 2: Lissajous figures (from the Documentation on `Manipulate`).

Example 3: Mathematica knows Markov processes. Discrete Markov Process

Basics: Functions

Mathematica is (mostly) dynamic. You do not need to "declare" variables or bother with types (Mathematica does not have types).
Variables are:
* typeless and mutable
* actually just functions with zero arguments
* global by default, so you should avoid mutation unless absolutely necessary
* saved in memory until you quit Mathematica or explicitly cleared

Functions are easy to declare using pattern matching.
Square brackets ‘[ ]’ are reserved for function application.

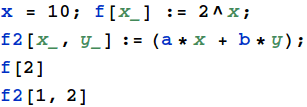
Two common newbie mistakes are forgetting the ‘:’ or the ‘_’ symbols.

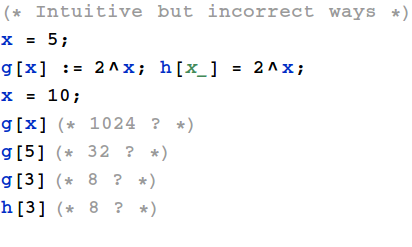
We can declare anonymous functions (== lambdas) using ‘#’ (slot) and ‘&’.
These are called “pure functions” in Mathematica.
(These can have side-effects, unlike pure functions in other functional languages)

You can make pure functions by literally calling `Function`.
(The '&' earlier is simply syntactic sugar for `Function`.)

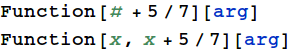
Pure functions can also be declared with multiple arguments.

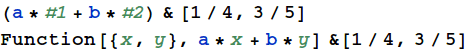
Mathematical equations are relatively easy to write and easy to read.
You cannot use '_' in function names as it is reserved for pattern matching.

You can use pattern matching to declare functions in a piece-wise manner.

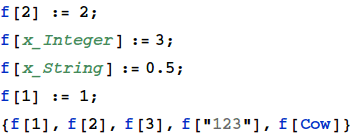
You can declare multi-expression functions using ‘;’ (`CompoundExpression`).
The function’s return value is the value of the expression after the last ‘;’.

Recall that variables and functions are global by default.
You can restrict the scope of temporary variables using `Module`
instead of using `Clear` all the time.

Basics: Lists and associations

Lists are the primary data structure in Mathematica.
Mathematica 10 introduces Associations, which are key-value pairs (dictionaries).
A lot of mathematical functions are ‘Listable’ i.e. they operate on lists automagically.

`Apply` splits a list into elements and feeds them as arguments to a function.

Some other useful functions to operate on lists are `Map`, `Thread`, `MapThread`, and `Transpose`.

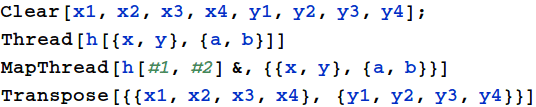
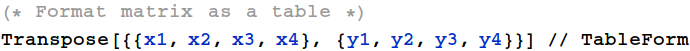
// is just postfix notation for unary function application, like @ was prefix notation for the same.

List indices start at 1. Indexing is done using double brackets '[[ ]]' or 'Part[list, ind]'.

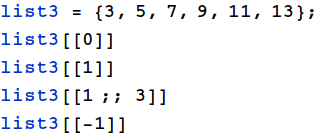
Since the brackets start increasing quickly with indexing and function application,
it is a good idea to avoid direct indexing for readability.

Associations are key-value pairs. Many functions that operate on lists also work on Associations.

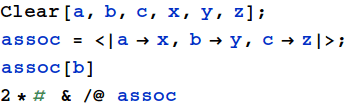
Interlude: `Manipulate`, `Animate`, `Plot3D`

`Manipulate` is useful for making interactive plots with sliders and other elements.

It is also relatively easy to make animations.

3D plots are easy to make and can be rotated directly without special commands.

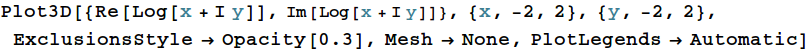
Basics: Getting help

Mathematica has a built-in documentation centre accessible using F1 or under the Help Menu.

Say I have code which I copy pasted below which I don’t fully understand.

There is also a dedicated Mathematica StackExchange which will almost always have an answer
for all your basic questions (use the search function!). People are usually happy to help and fairly polite.

MUST-READ: https://mathematica.stackexchange.com/questions/18393/what-are-the-most-common-pitfalls-awaiting-new-users

Basics: Control flow

Control-flow keywords like ‘if’, ‘do’, ‘for’ etc. are just ordinary functions in Mathematica.
Therefore, unlike many other languages, `If` actually returns a value.
(Recall: All functions return values)

Despite that, in most cases you want to avoid writing a loop structure.
If you are writing a `For` loop as a beginner, you are almost surely doing something wrong!

Example 1: Sum all triangular numbers (Tn) below a given M. One definition is Tn = n(n+1)/2.

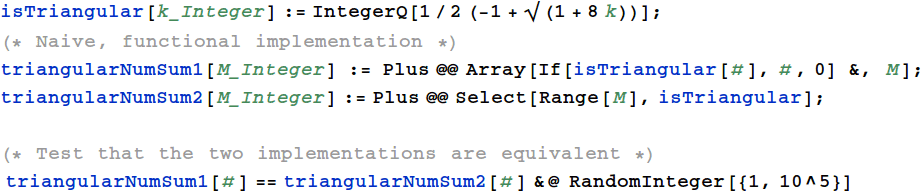
The implementation is bad because it wastes time doing checks for all numbers.
If we were writing imperative code, we could change the logic to:
* Start a `For` loop with n=1 (iteration variable), Σ=0
* Compute Tn = n(n+1)/2.
* If Tn ≤ M, then increment Σ by Tn, else break.

Can this be written in a functional style?

Example 2: Can we convert the following pseudo-code into a more functional style?

for (x,y) in XYpairs:
    y = foo(x)
    total += bar(x,y)

How can we get rid of the ‘for’ loop? Wouldn’t using `Map` force us to iterate through the list twice?

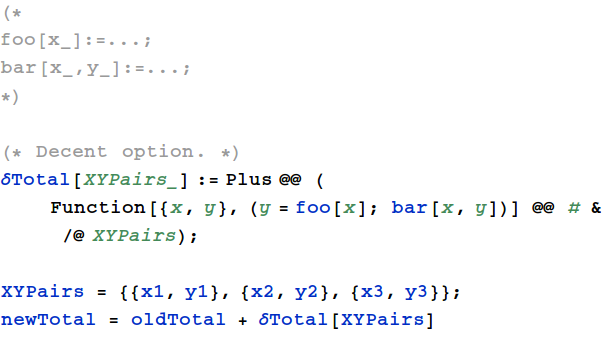
XYPairs was mutated inside δTotal, which may not be immediately obvious
while refactoring, especially for bigger, intimidating functions.

Instead, try to avoid mutating arguments as far as possible.
Mathematica can memoize function values if the function has no side-effects.
Most library functions, even those named as `Append`, avoid mutating arguments.
(there is an additional function `AppendTo` as an option.)

Learn to use functions like `Map`, `Array`, `MapThread`, `Transpose`, `Apply`, `Select` (== filter) etc.
that operate on entire lists instead of writing loops.

Bonus: You can call WolframAlpha from Mathematica

    1    https://stackoverflow.com/questions/4558732/is-mathematica-an-untyped-language